En este artículo explicaremos como se crean los patrones de sombras en CE3X sobre una cubierta plana.
Se estudiarán 2 casos diferentes:
A) Sombra sobre una cubierta plana que produce un casetón del mismo edificio o un edificio anexo de mayor altura.
B) Sombra sobre una cubierta plana que produce un toldo horizontal ubicado en el mismo edificio.
Se estudiarán 2 casos diferentes:
A) Sombra sobre una cubierta plana que produce un casetón del mismo edificio o un edificio anexo de mayor altura.
B) Sombra sobre una cubierta plana que produce un toldo horizontal ubicado en el mismo edificio.
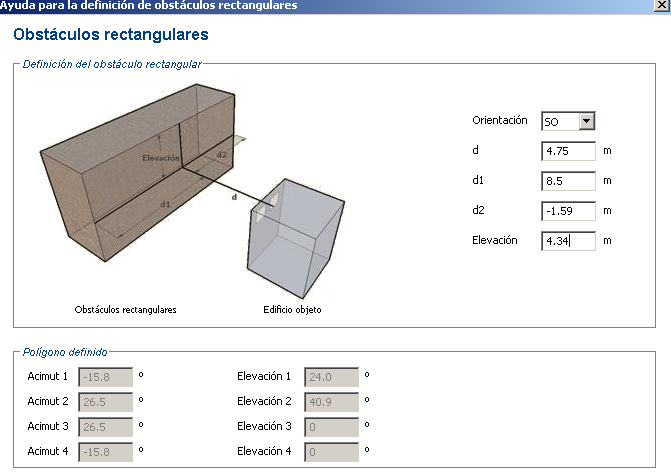
A) Sombra sobre una cubierta plana que produce un casetón del mismo edificio o un edificio anexo de mayor altura.
Para este ejemplo se empleará el Procedimiento de Introducción Simplificada del que dispone el programa.
Para este ejemplo se empleará el Procedimiento de Introducción Simplificada del que dispone el programa.
El procedimiento que debemos seguir es el siguiente:
1) Marcamos el punto de referencia (PR) de la edificación que estamos estudiando. Es el centro geométrico de la cubierta.
1) Marcamos el punto de referencia (PR) de la edificación que estamos estudiando. Es el centro geométrico de la cubierta.
2) Desde PR trazamos una línea perpendicular al plano donde se encuentra el obstáculo que vamos a estudiar. El punto de intersección de la recta con el plano lo llamaremos (PO). El punto PO puede estar, según cada caso, dentro del obstáculo o fuera de él.
3) Medimos el ángulo de desviación respecto del Sur de la recta que une los puntos PR y PO. Con este ángulo obtenemos la orientación que debemos considerar.
En este caso, en ángulo es de 44º (con signo positivo puesto que es hacia el Oeste), por lo que la orientación sería Suroeste.
En este caso, en ángulo es de 44º (con signo positivo puesto que es hacia el Oeste), por lo que la orientación sería Suroeste.
4) Medimos la longitud de la recta que une los puntos PR y PO. Esta longitud es el parámetro "d" que debemos introducir.
En este caso, el valor de "d" es 4,75.
En este caso, el valor de "d" es 4,75.
5) Medimos la longitud desde el punto PO hasta A1 que es la arista del obstáculo que está hacia el Este (viendo desde el punto PR hacia el obstáculo, la que está hacia la "izquierda"). Esta longitud es el parámetro "d1" que debemos introducir.
En este caso, el valor de "d1" es 8,50.
En este caso, el valor de "d1" es 8,50.
6) Medimos la longitud desde el punto PO hasta A2 que es la arista del obstáculo que está hacia el Oeste (viendo desde el punto PR hacia el obstáculo, la que está hacia la "derecha"). Esta longitud es el parámetro "d2" que debemos introducir.
En este caso, el valor de "d2" es 1,59. ¡Ojo! Lo introduciremos con valor negativo puesto que lo hemos tenido que medir hacia la izquierda (tomando como referencia PO) en lugar de hacia la derecha.
En este caso, el valor de "d2" es 1,59. ¡Ojo! Lo introduciremos con valor negativo puesto que lo hemos tenido que medir hacia la izquierda (tomando como referencia PO) en lugar de hacia la derecha.
7) Medimos en el alzado la elevación del punto más alto del obstáculo respecto del punto PR. Esta longitud es el parámetro "elevación" que debemos introducir.
En este caso, el valor de "elevación" es 4,34.
Una vez introducidos todos los valores, el patrón que obtenemos es este:En este caso, el valor de "elevación" es 4,34.
Debemos tener en cuenta que también habría que introducir en el mismo patrón otro obstáculo, que es el plano donde estan las aristas A2 y A3.
B) Sombra sobre una cubierta plana que produce un toldo horizontal ubicado en el mismo edificio.
Para este ejemplo se empleará la introducción por ángulos.
El procedimiento que debemos seguir es el siguiente:
1) Marcamos el punto de referencia (PR) de la edificación que estamos estudiando. Es el centro geométrico de la cubierta.
Además marcamos los vertices superiores del toldo (puntos 1 a 4).
2) Trazamos la línea de Sur, desde el punto PR.
Además trazamos líneas desde PR a cada uno de los 4 vertices superiores del toldo.
Medimos los ángulos de azimut (alfa) de los 4 puntos (el ángulo que forma cada liíea de las que hemos trazado respecto del Sur). Los ángulos hacia el Este los tomaremos con valor negativo y hacia el oeste con valor positivo.
En este caso obtenemos:Además trazamos líneas desde PR a cada uno de los 4 vertices superiores del toldo.
Medimos los ángulos de azimut (alfa) de los 4 puntos (el ángulo que forma cada liíea de las que hemos trazado respecto del Sur). Los ángulos hacia el Este los tomaremos con valor negativo y hacia el oeste con valor positivo.
Punto 1 - Alfa 1= -37º
Punto 2 - Alfa 2= -28º
Punto 3 - Alfa 3= 11º
Punto 4 - Alfa 4= -10º
3) Medimos las distancias en planta (proyección en planta) desde cada punto hasta PR, las denominaremos Dref. Esto nos da la dimensión del cateto contiguo para calcular los ángulos de elevación (beta) de cada punto.
El valor del cateto opuesto de esos ángulos es el mismo para todos, e igual a la altura del toldo (3,00 m).
El valor del cateto opuesto de esos ángulos es el mismo para todos, e igual a la altura del toldo (3,00 m).
Por lo tanto, aplicando trigonometría podemos calcular los valores de los angulos de elevación (beta):
Beta1= arctang(3,00/9,62) = arctang(0,31) = 17,20º
Beta2= arctang(3,00/4,74) = arctang(0,63) = 32,21º
Beta3= arctang(3,00/8,32) = arctang(0,36) = 19,80º
Beta4= arctang(3,00/11,80) = arctang(0,25) = 14,03º
Beta1= arctang(3,00/9,62) = arctang(0,31) = 17,20º
Beta2= arctang(3,00/4,74) = arctang(0,63) = 32,21º
Beta3= arctang(3,00/8,32) = arctang(0,36) = 19,80º
Beta4= arctang(3,00/11,80) = arctang(0,25) = 14,03º
Una vez introducidos todos los valores, el patrón que obtenemos es este:
















Muy buen post. Perfectamente explicado.
ResponderEliminarMI enhorabuena!
Muchas gracias por leer el blog y comentar.
EliminarUn saludo
Hola! Muy buen post y muy claro todo, al igual que otros post que acostumbro a leer en esta web. Veo que este método de obtener el patrón de sombras sobre las cubiertas planas es el mismo que el comentado en otro post para las sombras de fachadas. Tiene sentido puesto que se parte a través de un punto lanzado perpendicularmente.
ResponderEliminarAhora bien, tengo una duda, ¿Este método del patrón de sombras para las cubiertas planas se puede utilizar del mismo modo para cubiertas inclinadas (teja cerámica curva)? Imagino que sí, bajo mi punto de vista, la única diferencia estaría en la "elevación" que pide el programa puesto que los faldones de esta tipología de cubiertas son inclinadas y por tanto se podría partir la "elevación" a partir de una altura media de dichos faldones. Creo y por eso pregunto, que al ser el programa CE3X un procedimiento simplificado, esto se podría realizar.
Otra duda que tengo es la siguiente: ¿El patrón de sombras para las cubiertas sólo se aplicaría en el caso de realizar el certificado de eficiencia energética a un edificio completo o en el caso de que la vivienda individual que se certifique corresponda con la última vivienda del edificio verdad?
Muchas gracias ya de antemano por sus respuestas. Estoy muy agradecido por su blog. Sin duda de lo mejor que hay por internet.
Buenos días, Iván:
Eliminar1) Tal y como tu dices, yo entiendo que una cubierta inclinada se podría modelizar como si fuese plana tomando como elevación la altura media de los faldones.
2) El patrón de sombra se aplicaría en los dos casos que planteas: tanto si certificas la vivienda del bajocubierta, como si certificas el edificio completo.
3) En todo caso, debemos tener en cuenta que dicha sombra solo influirá (en mayor o menor medida) en la certificación en el caso de que en la cubierta existan lucernarios o huecos.
Muchas gracias por tu interés en los artículos y tus comentarios.
Un saludo
Muy buen post, pero me surge una duda, en el caso de que el obstáculo que produzca sombra sea un poligono de mas de cuatro lados, tendrimos mas de cuatro puntos de referencia, ¿como los introduciríamos en el programa?
ResponderEliminarMuy buen post, pero me surge una duda. En el caso que el obstáculo que produzca sombra esté formado por un polígono de más de cuatro lados (habría mas de cuatro puntos de referencia) ¿Como introducimos estos en el programa?
ResponderEliminarUn saludo
Buenos dias, Fernando:
EliminarEn ese caso entiendo que tendríamos dos soluciones posibles:
1) La vía rápida sería simplificar el poligono para convertirlo en uno de cuatro lados similar al que tenemos.
2) La otra solución sería dividir el polígono objeto en varios poligonos de cuatros lados (dos o mas polígonos, dependiendo del numero del poligono objeto)
Un saludo y gracias por tus comentarios.
JLCM